The atmosphere transports heat throughout the globe extremely well, but present-day atmospheric characteristics prevent heat from being carried directly from the equator to the poles. Currently, there are three distinct wind cells - Hadley Cells, Ferrel Cells, and Polar Cells - that divide the troposphere into regions of essentially closed wind circulations. In this arrangement, heat from the equator generally sinks around 30° latitude where the Hadley Cells end. As a result, the warmest air does not reach the poles. If atmospheric dynamics were different, however, it is plausible that one large overturning circulation per hemisphere could exist and that wind from the low-latitudes could transport heat to the high-latitudes. As an explanation for equable climates, Brian Farrell presented this idea in 1990 and advocated that during equable climates, the Hadley Cells extended from the equator to the poles (Farrell, 1990).

Atmospheric Wind Cells

Hadley cells, Ferrel (mid-latitude) cells, and Polar cells characterize current atmospheric dynamics.

Hadley Cells are the low-latitude overturning circulations that have air rising at the equator and air sinking at roughly 30° latitude. They are responsible for the trade winds in the Tropics and control low-latitude weather patterns. Held and Hou (1980) outlined the dynamics of this circulation through a simplified model of the Hadley Cell. For the model, there are three main assumptions. First, the Hadley Cell circulation is constant. Second, the air moving toward the poles in the upper atmosphere conserves its axial angular momentum, while the surface air moving equatorwards is slowed down by friction. Third, the thermal wind balance holds for the circulation (Vallis, 2006). For simplicity, the model is also symmetric around the equator. These initial assumptions make the explanation of Hadley Cell dynamics much simpler.

Angular momentum is defined as the cross product of a particle's distance from the axis of rotation, r, and the particle's linear momentum, p. In the Hadley Cell as an air particle moves toward the high-latitudes, it becomes closer to the Earth's spin axis, so r becomes smaller. If angular momentum is conserved in the Hadley Cell as Held and Hou (1980) assume, p must become larger to balance the decrease in r. P equals mass times velocity. Since the mass of the air particle cannot change, the velocity of the particle must increase. In the case of the Hadley Cell, the velocity in question is the zonal (east-west) velocity, so as the particle moves poleward, the velocity must increase in the eastward direction. Eventually, the zonal velocity is so strong that the particle stops moving poleward and only travels to the east. At this latitude, air sinks, and then to close the loop, it returns to the equator along the surface. Therefore, because of the conservation of angular momentum, Hadley Cells exist only from the equator to the mid-latitudes.

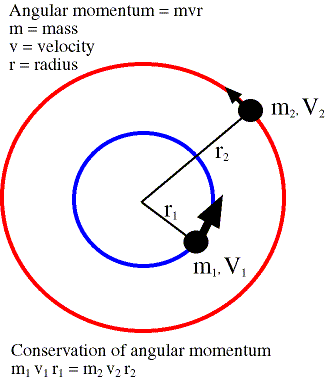
Angular Momentum

To conserve angular momentum, velocity must increase as the radius decreases. (Image courtesy of Lyndon State College Atmospheric Sciences)

This scenario holds as long as the initial assumptions are valid. Brian Farrell, however, argues that the assumptions are not accurate for equable climates and that during equable climates, angular momentum is not conserved in poleward moving particles (1990). He claims that angular momentum sinks, essentially sources of friction, could have been stronger during the Eocene and the Cretaceous. Farrell estimates that the friction term in his model would increase by eightfold under equable climate conditions. This change would prevent angular momentum from being conserved. In this situation, the zonal velocity would not become strong enough to stop air from moving poleward. Instead, air from the equator would be able to travel all the way to the poles in extended Hadley Cells.

Based off of Venus' atmosphere's behavior, Farrell argues that another way to extend the Hadley Cells would be to increase the height of the tropopause. This change would increase the poleward moving air's Rossby number. The Rossby number describes the importance of the Coriolis force in atmospheric dynamics. A higher Rossby number means that the Coriolis force has a smaller impact on a particle, so if the height of the tropopause increased enough, the Rossby number would become high enough to make the Coriolis force negligible. As a result, particles would not diverge from their path as they moved poleward, and the Hadley Cells would reach the poles. To explain how the tropopause height could increase, Farrell states that the height is correlated to surface temperature and that a 1°C increase in sea surface temperature causes the tropopause potential temperature to rise by roughly 7.5°C. Raising the average equatorial sea surface temperature to 32°C from its current 27°C would increase the potential temperature of the tropopause by 37°C. There temperature increases would almost double the static stability at the tropopause. For the height to increase, the stratosphere would also have to become less stable. If CO2 concentrations increased and if stratospheric ozone concentrations decreased, the stratosphere would cool substantially, and this change would destabilize the stratosphere. As a result of the alterations to tropospheric and stratospheric stability, the tropopause height would increase. Farrell estimates the height would have doubled under Cretaceous conditions, and as a result, the Rossby number would have doubled. This change would have allowed the Hadley Cells to extend to the poles and would have made equable climates more likely.

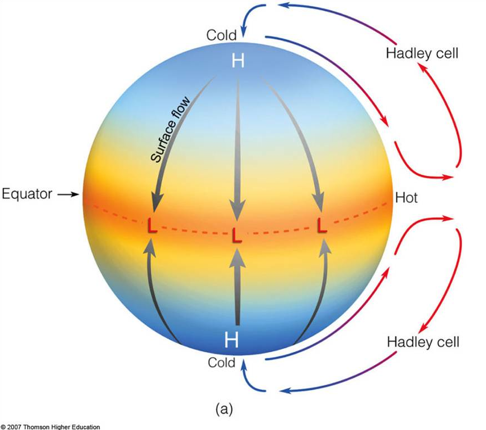
Hadley cells extended all the way to the poles

Hadley cells could extend all the way to the poles. (Image courtesy of Lyndon State College Atmospheric Sciences).

While each of these alterations to the atmosphere would extend the Hadley Cells, Farrell found that a combination of the two effects was necessary to make his model's results agree with proxy data from equable climates. He graphed the atmosphere's potential temperature versus latitude at different tropopause height and friction values. The results reveal that as tropopause height and friction increase, the EPTD decreases. A doubling of the tropopause height combined with an eightfold increase in the friction term leads to an EPTD of 16°C. This value agrees with Cretaceous climate reconstructions. As a result, Farrell's theory seems to be a reasonable explanation for equable climates.

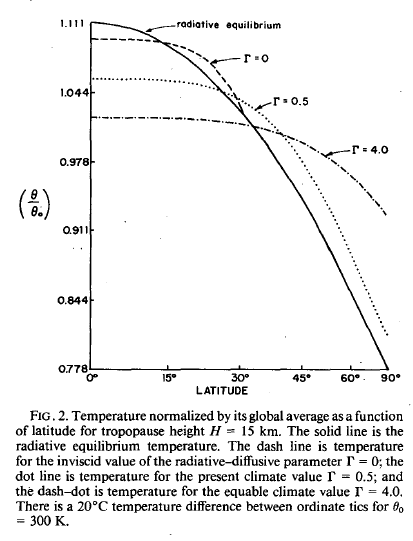
Potential Temperature vs. Latitude at Tropopause Height = 15 km
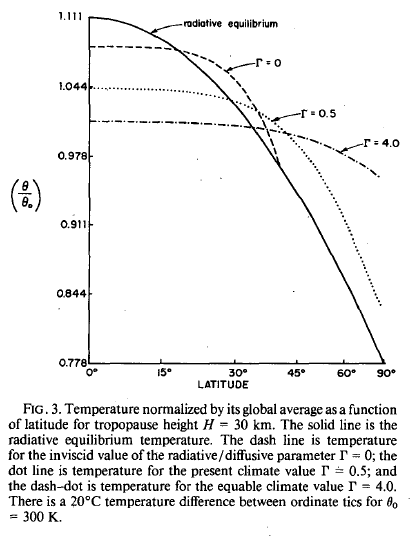
Potential Temperature vs. Latitude at Tropopause Height = 30 km

Farrell's results show that as the friction term (Γ) and the tropopause height increase, the EPTD decreases. (Farrell, 1990)

The main problem is that Farrell does not provide any explanation for why angular momentum sinks would have become stronger during the Cretaceous and the Eocene. He provides a few examples of potential momentum sinks: "small scale diffusion..., cumulus momentum flux..., gravity wave drag..., and the net westward force arising from potential vorticity mixing by large scale waves" (Farrell, 1990). However, he does not explain why any of these sinks would have become stronger during the Eocene and, thus, would have prevented angular momentum from being conserved. This lack of information in the argument makes the theory harder to accept, and until this portion of the argument is explored in greater depth, Farrell's theory cannot be accepted as the correct explanation of equable climates.

This qualitative explanation supplies the fundamental ideas of Farrell's theory, but to fully understand it, a quantitative approach is necessary. To see the mathematical approach used as the fundamental basis for this theory, click here.